Compuertas logica

Compuerta NAND:La salida es alta (1), cuando cualquiera de las entradas A ó B es alta, o cuando ninguna es alta. En otras palabras, la salida es normalmente alta, solo es baja cuando ambas entradas son altas.



Compuerta NOR:La salida es alta solamente cuando ninguna de las entradas ni A ni B sean altas. Es decir, la salida normalmente está alta, pero cualquier clase de entrada que no sea cero la llevara a baja.

Compuerta logicas

Compuerta OR, puerta lógica digital que implementa la disyunción lógica. Se utiliza para conectar dos o más variables, y basta con que una de las variables se cumpla para que toda la función sea verdadera. El operador se representa por el símbolo " + " el cual se lee "o". Expresándolo en otras palabras: En una compuerta OR, la salida será "1", cuando en cualquiera de sus entradas haya un "1".


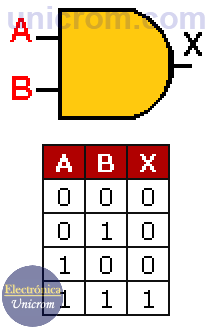
Compuerta AND:La compuerta AND o compuerta Y lógica es una de las compuertas más simples dentro de la Electrónica Digital. Su representación o símbolo es la que se muestra en las siguientes figuras.

La compuerta Y lógica más conocida tiene dos entradas A y B, y aunque puede tener muchas más (A,B,C, etc.) sólo tiene una salida: X.

Compuerta logica

Las compuertas lógicas son circuitos electrónicos diseñados para obtener resultados booleanos (0,1), los cuales se obtienen de operaciones lógicasbinarias (suma, multiplicación). Dichas compuertasson AND, OR, NOT, NAND, NOR, XOR, XNOR.

Compuerta NOT

En lógica digital, un inversor, puerta NOT o compuerta NOT es una puerta lógica que implementa la negación lógica . A la derecha se muestra la tabla de verdad. Siempre que su entrada está en 0 (cero) o en BAJA, su salida está en 1 o en ALTA, mientras que cuando su entrada está en 1 o en ALTA, su SALIDA va a estar en 0 o en BAJA.

Algebra Booleana

---

🔍 ¿Qué es el Álgebra Booleana?

Es una rama especial del álgebra que se usa principalmente en electrónica digital. El álgebra booleana fue inventada en el año 1854 por el matemático inglés George Boole.

El álgebra de Boole es un método para simplificar los circuitos lógicos (o a veces llamados circuitos de conmutación lógica) en electrónica digital.

Por lo tanto, también se llama como "Cambio de álgebra". Podemos representar el funcionamiento de los circuitos lógicos utilizando números, siguiendo algunas reglas, que son bien conocidas como "Leyes del álgebra de Boole".

También podemos hacer los cálculos y las operaciones lógicas de los circuitos aún más rápido siguiendo algunos teoremas, que se conocen como "Teoremas del álgebra de Boole". Una función booleana es una función que representa la relación entre la entrada y la salida de un circuito lógico.

La lógica booleana solo permite dos estados del circuito, como True y False. Estos dos estados están representados por 1 y 0, donde 1 representa el estado "Verdadero" y 0 representa el estado "Falso".

Lo más importante para recordar en el álgebra de Boole es que es muy diferente al álgebra matemática regular y sus métodos. Antes de aprender sobre el álgebra de Boole, vamos a contar  un poco sobre la historia del álgebra de Boole y su invención y desarrollo.

Resta de Binario

La resta o sustracción de números binarios es similar a los números decimales. La diferencia radica en que, en binario, cuando el minuendo es menor que el sustraendo, se produce un préstamo o borrow de 2, mientras que en decimal se produce un préstamo de 10.

Al igual que en la suma, el proceso de resta binaria, se inicia en la columna correspondiente a la de los dígitos menos significativos. En la figura 5 se indican las reglas que rigen la resta binaria y en la figura 6 se muestra un circuito lógico, llamado semirrestador (HS), que sustrae un B de un bit A y suministra un bit de diferencia (Di) y un bit de préstamo (Bo).

Suma de Binario

La tabla de sumar, en binario, es mucho más sencilla que en decimal. Sólo hay que recordar cuatro combinaciones posibles.

Como ejemplo:

Es tan sencilla como sumar en decimal, aplicando la tabla que se encuentra encima. Pero la suma de 1+1, que sabemos que es 2 en el sistema decimal, debe escribirse en binario con dos cifras (10) y, por tanto 1+1 es 0 y se arrastra una unidad, que se suma a la posición siguiente a la izquierda, se conoce como bit de acarreo.

En el caso de la suma en binario puro con signo en complemento a 2 consiste en sumar las secuencias binarias según la regla del binario puro, despreciando el acarreo final y teniendo en cuenta que habrá desborde si los dos últimos acarreos son distintos.

Binario a Hexadecimal--Hexadecimal a Binario

Del mismo modo que hallamos la correspondencia entre números octales y binarios, podemos establecer una equivalencia directa entre cada dígito hexadecimal y cuatro dígitos binarios, como se ve en la siguiente tabla:

DECIMAL	BINARIO	HEXADECIMAL
0	0000	0
1	0001	1
2	0010	2
3	0011	3
4	0100	4
5	0101	5
6	0110	6
7	0111	7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F

Binario a hexadecimal:

La conversión entre números binarios y hexadecimal se realiza "expandiendo" o "con­trayendo" cada dígito hexadecimal a cuatro dígitos binarios. Por ejemplo, para expresar en hexadecimal el número binario 101001110011₂ bastará con tomar grupos de cuatro bits, empezando por la derecha, y reemplazarlos por su equivalente hexadecimal: 

1010₂ = A₁₆

0111₂ = 7₁₆

0011₂ = 3₁₆

y, por tanto: 101001110011₂ = A73₁₆

En caso de que los dígitos binarios no formen grupos completos de cuatro dígitos, se deben añadir ceros a la izquierda hasta completar el último grupo. Por ejemplo:

101110₂ = 00101110₂ = 2E₁₆

_{Hexadecimal a binario:}

La conversión de números hexadecimales a binarios se hace del mismo modo, reemplazando cada dígito hexadecimal por los cuatro bits equivalentes de la tabla. Para convertir a binario, por ejemplo, el número hexadecimal 1F6₁₆ hallaremos en la tabla las siguientes equivalencias:

1₁₆ = 0001₂

F₁₆ = 1111₂

6₁₆ = 0110₂

y, por tanto: 1F6₁₆ = 000111110110₂